notes

Engineering Systems Architecture

Instructors - Peter Jackson, Stefano

• Engineering Systems Architecture
  • Grading Breakdown
  • Midterms revision
    • Architectural design concepts
    • Identifying Stakeholders
    • Influence Diagrams
    • Architectural DSM
    • Modularity
    • Trade Studies
  • Finals revision
    • Architectural Trade-spaces (L13, W8)
    • Visualizing Complex Decision Spaces (L14, W9)
    • Choosing Among Multiple Solutions (L15, W9)
    • Generating Multiple Solutions (L16-L18, W10-W11)
    • Evolutionary and Genetic Algorithms (L19-L20, W11-W12)

Our documentation and demo may be included.

Grading Breakdown

Component	Weightage (%)
Class participation	10
Project (System definition)	20
Project (R-Shiny)	25
Mid-term Exam	20
Final Exam	25

Deadlines

• Week 9 - HTML portfolio of documents detailing steps in the architectural design process, with their outputs; maximal use of Capella where possible
• Week 13 - A game enhancement mechanism delivered using RShiny; Working prototype of design concept; 3-minute video with marketing pitch for design concept

(develop an educational game)

Project Theme

• Design an educational game (or toy).
• Teams of four
  • Made up of two partners
  • You can choose three people that can be your partner

Midterms revision

Bring a ruler to improve your quality of life.

Architectural design concepts

• Modularity, Operational Analysis, Scenario Analysis, Structural Design, Operational Analysis, Concept Generation, Problem and Mission Statements, Use Cases
• Use common sense

Identifying Stakeholders

• Your power-interest diagram require annotated arrows.

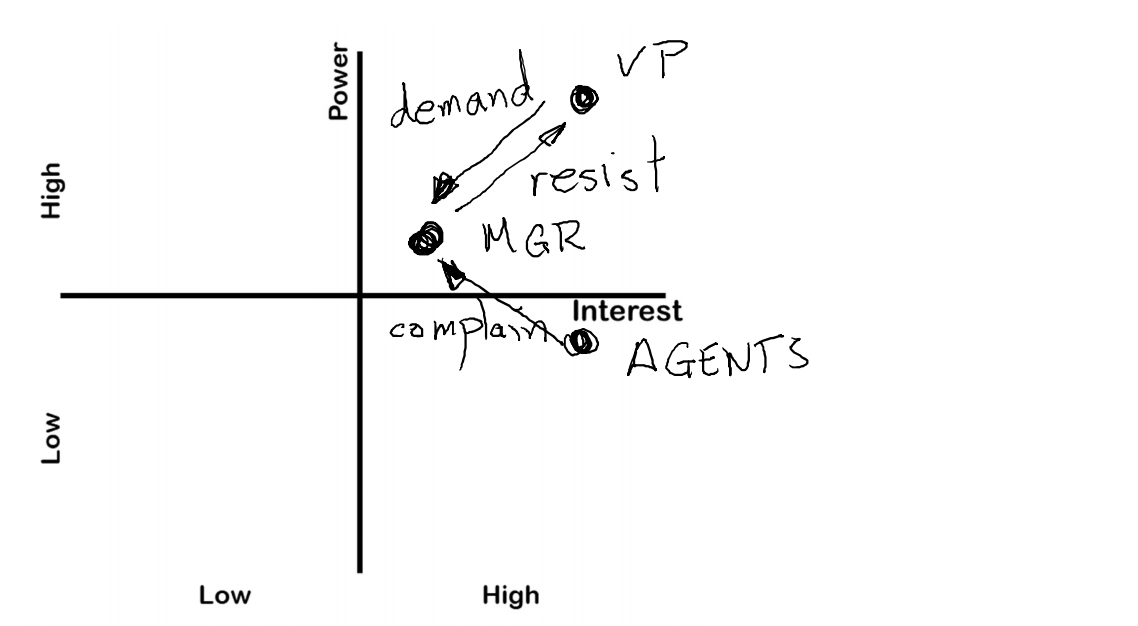
• One table explains the position of the power and interest in the diagram.
• One table explains the relationship between the different stakeholders. You only need to fill up cells with a relationship.

Influence Diagrams

• Sketch this argument using the Design Research Methodology notation. In particular, each arc should have two signs (either “+” or “-“), one at the tail end of the arc and the other at the head of the arc. Label each arc as “E”, for “Experience” or “A” for “Assumption”.
• Points will be deducted if you use the words “increase” or “decrease” within a bubble - this information belongs on the arcs.
• Your proposal should be in the shape of a hexagon.

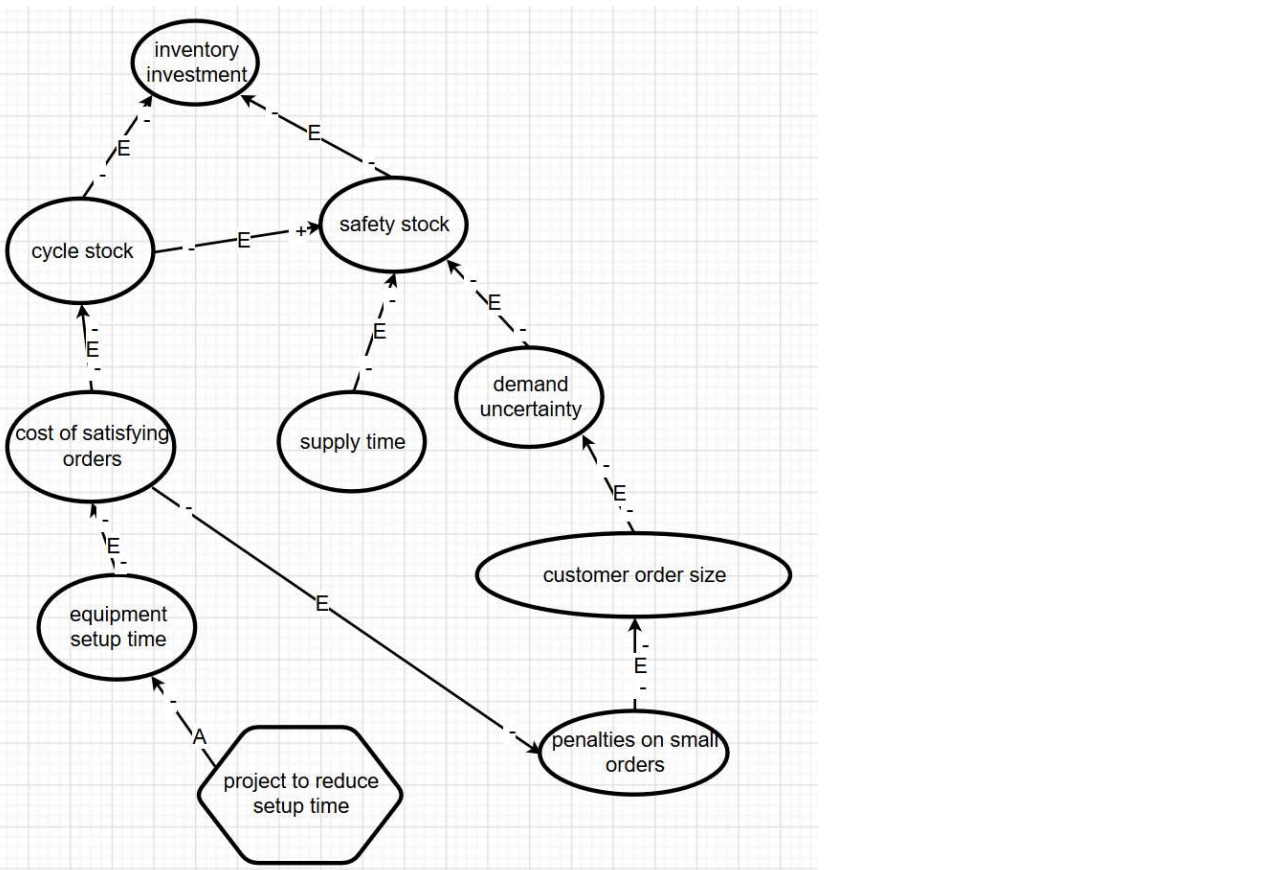
Architectural DSM

• Rearrange rows and columns such that the “loss” is minimum. “Loss” is the distance of ones from the diagonal.
• You can sketch the relationships as a graph.

Modularity

• Identify six functions
• Identify three subsystems
• Assign functions to the subsystems
• List the exchanges on a table “Exchange”, “From Entity”, “To Entity”
• Sketch a state change diagram for a typical cycle of events

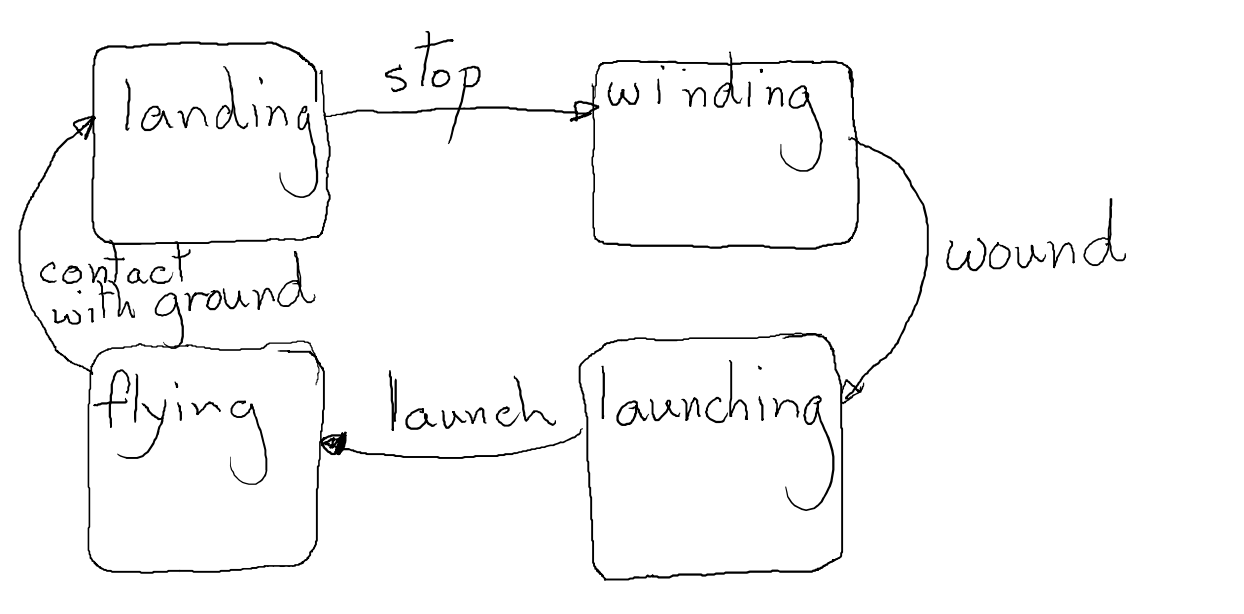
Trade Studies

• You need to draw a table.
• Headings: Attribute List, Relative Weighting, A Rating, A Weighted Rating, B Rating, B Weighted Rating.
• Summaries (after attribute list): Total, Rank, Recommend

Finals revision

This is a summary of the second half of the course. The finals is focused on R programming.

Installation script (not exhaustive, someone should complete this)

install.packages('ggplot2')
install.packages('devtools')
install.packages('devtools')
devtools::install_github('r-lib/later')
install.packages('shiny')

Architectural Trade-spaces (L13, W8)

Multi-Objective Problem

You minimise a vector (instead of a value) in a minimisation optimisation problem.

Nadir point is not the worse vector in the feasible region. It represents the upper bound of objective elements of the objective vector in the Pareto optimal set.

A solution weakly dominates over another solution if

• The solution is not worse in all objectives
• The solution is strictly better in at least one objective

Strongly dominates if

• The solution is strictly better in all objectives

Properties of domination

• Not reflexive - you cannot dominate yourself
• Not symmetric - domination is one way
• Transitive - if $a$ dominates $b$, and $b$ dominates $c$, $a$ dominates $c$.

The Pareto optimal set is the set of optimal solutions that are not dominated by any other solution in the feasible space.

Visualizing Complex Decision Spaces (L14, W9)

• Parallel coordinates

• Radar plots

Choosing Among Multiple Solutions (L15, W9)

• Lexicographic method
  • an objective with lower-level priority is (infinitely) less important than an objective with a higher-level priority
• Utopia point method
  • choose the closest solution to the Utopia point
  • recommended to normalize the data to within $[0,1]$
    • $f_i^{norm} = \dfrac{f_i - f_i^}{f_i^{nad} - f_i^}$
• Maximum curvature method
  • the point in which the Pareto front curvature is maximum
  • tradeoff is less reasonable at other points

Generating Multiple Solutions (L16-L18, W10-W11)

A-posteriori method

• No information about the decision-maker’s preference structure is available. They iteratively generate a set of Pareto-optimal solutions

Interactive methods

• Use the information progressively during the optimization process

A-priori methods

• Some information is available. They usually find one preferred Pareto-optimal solution

$\varepsilon$-constraint methods (a-posteriori)

• Please revise on code

Weighting method (a-posteriori)

• Combine all objectives into a single objective function by assigning weights to each objective. The sum of weights is usually one
• You need to scale your objective function with nadir and utopian vector (really?)
• You may not find the Pareto frontier if the feasible space is non-convex

Goal programming (a-priori)

• There is a goal for each objective
• To minimize positive and negative deviations from the goals
• Uses and minimises “slack variables”

Lexicographic Goal Programming (a-priori)

• Lexicographic method - but positive and negative deviations are prioritised differently
• Unwanted deviations are placed into a number of priority levels
• Some goals are defined more important than the others
  • Some goals can share the same priority

Weighted Goal Programming (a-priori)

• The achievement function consists of a weighted (normalized) sum of unwanted deviations

Interactive methods

• NIMBUS
• The idea is to move around the Pareto optimal set
• When a solution is presented, the decision maker decides for each objective function
  • Should be improved
  • Should be improved till some aspiration level
  • Are satisfactory at the moment (no change)
  • Are allowed to impair till some bound
  • Are allowed to change freely

Evolutionary and Genetic Algorithms (L19-L20, W11-W12)

• A heuristic is a technique designed for solving a problem more quickly when classic methods are too slow, etc. A metaheuristic are problem-independent methods

Key elements

• Group of Individuals - Population
• Source of Variation - Genetic operators
• Reproductive Fitness - Fitness
• Survival of the Fittest - Selection

Binary Genetic Algorithms

• Nonlinear optimisation algorithm
• Each solution is encoded in binary
• Procedures
  • Identify good (above average) solutions in the population;
  • Make multiple copies of good solutions;
  • Eliminate bad solutions from the population so that multiple copies of good solutions can be placed in the population.

Multi-objective Genetic Algorithms

• Objective
  • Identify the Global Pareto-Optimal set of solutions (aka the Pareto Optimal Front).
  • Find a sufficient coverage of that set.
  • Find an even distribution of solutions.

Non-dominated sorting genetic algorithm II, NSGA-II

• Main advantages
  • The diversity among non-dominated solutions is maintained using the crowding procedure: No extra diversity control is needed.
  • Elitism protects an already found Pareto-optimal solution from being deleted.