notes

Artificial Intelligence

Cheatsheet

cheatsheet-page-1

cheatsheet-page-2

cheatsheet-page-3

cheatsheet-page-4

Introduction to AI

Turing Test

Definitions of AI

Social impact of AI

The Agent Model

Agent - Anything that can be viewed as perceiving its environment through sensors and acting upon that environment through actuators

An agent function maps a sequence of percept vectors to an action.

A rational agent chooses whichever action that maximises the expected value of performance measure given the percept sequence to date and prior environment knowledge.

Different AI problems with the PEAS framework

Environment types

Problem Solving Agent Formulation

A solution is a sequence of actions from the initial state to the goal state. An optimal solution is a solution with the lowest path cost.

Evaluation Tree Search Graph Search
Data structures Recursion stack Frontier
Explored set
Memory Height of search tree All visited nodes
Time Expensive if graph is not a tree?
Intractable if graph is non acyclic?		 Number of nodes and edges
Comparison Redundant paths can cause the problem become intractable Potentially a large number of states of track

Evaluation of Search Strategies

Variables to evaluate space and time complexity

Uninformed search - no additional information about states beyond that in the problem definition. (i.e. searching blindly, no idea on the desirability of each state)

Search Algorithm General Idea Impl Complete Optimal Space Time
Breath-First Search Expand the shallowest unexpanded node Use a FIFO queue Yes (if finite) [0] Yes (if edge cost is constant) $O(b^d)$
[1]		 $O(b^d)$
Uniform-Cost Search Expand unexpanded node n with the lowest path cost g(n) [7] Using a priority queue ordered by path cost g [1b] Yes (if step cost > $\varepsilon$) [1a] Yes $O(b^{C^*/\varepsilon})$
[2]		 $O(b^{C^*/\varepsilon})$
[2a]
Depth-First Search (DFS) Expand the deepest unexpanded node Use a LIFO queue No (if infinite) No [3] $O(b^m)$ $O(bm)$
[4]
Depth-Limited Search (DLS) DFS with predetermined depth limit $l$ DFS but stop at $l$ No (if $l<d$) No (if $l<d$) $O(b ^l)$ $O(b l)$
Iterative Deepening Search Use increasing Depth-Limited Search (DLS) to find the best depth limit $l$ [5] Yes Yes (if edge cost is constant) $O(b^d)$ $O(bd)$

These are tree search algorithms. (How does these apply to graph search problems?)

Leetcode problems do not think of problems this way because graphs on Leetcode is constrained based on nodes and edges, rather than branching factor. Probably why this is confusing to me.

[0] Yes (if finite) - or rather “No (if infinite and does not have a solution)”?

[1] Do we need to store the path information?

[1a] Automatically penalises repeated paths. Does not prove no solution in infinite graph (can any algorithm do that anyway?)

[1b] In graph search, the state is added into the explored set only after expanding the node

[2] Consider a graph a-b-c-d, where b is the starting node and d is the goal state, and the cost of a-b and b-c is one, and the cost of c-d is large. We can see that the time uniform cost search is exponential wrt the cost of c-d.

[2a] Each insertion and removal cost $O(\log n)$ in the worst case. Is this considered in the complexity?

[3] The search might go down an infinite path, but the optimal solution may exist at a finite depth. Is this “No (if infinite)”?

[4] This is the maximum size of the LIFO queue will reach, keeping track of $b$ child nodes at each of the $m$ depths.

[5] Essentially BFS with better space complexity, but worse constant factor for time complexity.

[6] How do you know that a goal state is optimal? Does it assume an edge cost of one?

[7] How does UCS compare to Dijkstra https://www.baeldung.com/cs/uniform-cost-search-vs-dijkstras

Informed search - uses problem-specific knowledge beyond the definition of the problem itself (some idea of the desirability of each state)

Issue with uniform cost search - possible redundant searches and we may waste search in the wrong direction

Search Algorithm General Idea Complete Optimal Space Time
Uniform-Cost Search Expand unexpanded node n with the lowest path cost $g(n)$ Yes (if step cost > $\varepsilon$)
[1a]		 Yes $O(b^{C^*/\varepsilon})$ $O(b^{C^*/\varepsilon})$
Greedy Best-First search Expand unexpanded node n with the lowest heuristic value $h(n)$ No (potential of getting stuck in loops) No (optimal solution may not be greedy) $O(b^m)$ $O(b^m)$
A* search Expand unexpanded node n with the lowest $h(n) + g(n)$ Yes (same as UCS) Yes if heursitics are admissible Same as UCS Same as UCS

All algorithms above use a priority queue, and are tree search.

Heuristics $h(n)$ is an estimate of how close a state $n$ is to the goal state.

A heuristic is admissible if $h(n) \leq h^*(n)$

A heuristic is consistent if $h(n) \leq c(n, a, n’) + h(n’)$

A heuristic $h_2$ dominates another heuristic $h_1$ if $h_2(n) \geq h_1(n)$

How to design heuristics

Applications of A* search

Constraint Satisfaction Problems

Compared to standard search problems, CSPs are more interested in the goal rather than the sequence of actions (path)

Definition

Formulation

CSP Solution

Advantages of CSPs

Varities of CSP problems

CSPs as standard search problem

Backtracking

Example problem

{RGB} - {GB}
   |     | 
 {RG} - {G}

backtracking

(Backtracking with forward checking, diagram made by Shiying)

AC-3 algorithm

Arc consistency of $X \to Y$

Algorithm

V1 ---> V2: 	D1: RBG	D2: BG
V4 ---> V2: 	D4: G	D2: BG
V1 ---> V3: 	D1: RBG	D3: RG
V4 ---> V3: 	D4: G	D3: RG
V2 ---> V4: 	D2: B	D4: G  
(Delete G from V2, added V1->V2,	V4->V2)
V3 ---> V4: 	D3: R	D4: G
(Delete G from V3, added V1->V3,	V4->V3)

Complexity - $O(n^2 d^3)$

Performance

Tree-structured CSPs

Complexity - $O(nd^2)$

Algorithm

Nearly Tree-structured CSPs

Conditioning - instantiate a variable and prune its neighbours domains

Cutset conditioning - instantiate a set of variables such that the remaining constraint graph is a tree

Complexity - $O(d^c \cdot(n-c)d^2)$

(You can also condition a node to compute two separate graphs)

Adversarial search and games

Types of games

Representing a Game as a Search Problem

Minimax Algorithm

Approach

Performance

Simple fixes for the resource limit

Alpha-beta pruning

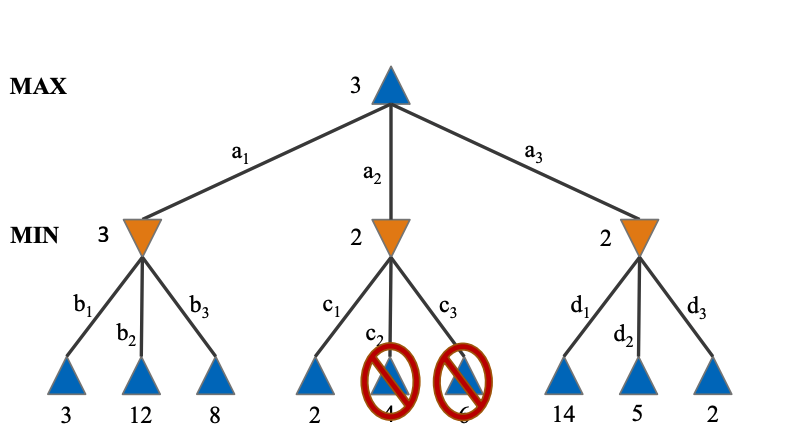
alpha-beta-pruning

For non-deterministic games

Machine Learning

Machine is the practice of using algorithms to learn from data. Previous approaches used rule based search.

There is still no general AI, all algorithms could only narrow tasks that they are designed on.

When is ML used

Components

Tasks and techniques

Types of learning

Designing a learning system

Evaluation

Sources of error

Total error = bias + variance + noise

Bridge set

Regularisation

Neural Networks

Concepts from Deep Learning

Convolutional Neural Networks

Deep Generative Models

Classical Planning

Planning is the process of computing several steps of a problem-solving process before executing any of them.

In search, states are represented as a single entity (which may be quite a complex object)

In planning, states have structured representation which are used by the planning algorithm

Types of planners

Classical planning - path-searching in a graph

STRIPS - Stanford Research Institute Problem Solver

STRIPS Instance definition (POIG)

Closed World Assumption - facts are not listed in a state are assumed to be false. The agent has full observability. Only positive facts need to be state. - is this applied on the initial state?

Examples - robot world, block world

Components of a PDDL task

Task specifications

Delete-relaxed problem

h+ heuristic

h-max

h-add

h-ff

Bayes and Uncertainty

Please know how to

Bayesian probability

General idea - “Compute distribution on query variable by fixing evidence variances and summing over hidden variables”

Inference by enumeration - count from the table

Use of conditional independence reduces the size of the representation of the joint distribution (joint distribution table) from $O(d^n)$ to linear in n. ($d$ is the largest domain size)

Conditional independence

How to count number of independent numbers needed - you do not double count $x$ and $1-x$

Probability of cause given effect and probaility of effect given cause

Bayesian network representation

Global semantics defines the full joint distribution as the product of local conditional distributions